CSBwin/DSA/Lesson 1: Difference between revisions
No edit summary |
m CSBwin/DSA Lesson 1 moved to CSBwin/DSA/Lesson 1 |
(No difference)
| |
Revision as of 16:31, 6 January 2009
- You probably recognize an algebraic formula like
1 + 2 * ( 3 + 4 )
which means to add 3 to 4, multiply the sum by 2 and add the product to 1. Notice that the operations take place in an order different than the order in which they are written. The parentheses cause 3 and 4 to be added before the multiplication by 2 and the \'operator precedence\' causes the multiplication by 2 to take place before adding 1. In a DSA, the operations always take place in the order written. So it looks a bit backward on paper.
How can we write this in the order that it is to take place? Like this?
3 + 4 * 2 + 1
?
WRONG!
NO! There are three operations and they happen in the correct order but when the first plus sign is encountered, it does not yet know what two things are to be added. Pretend you are typing this formula into the computer. As you enter each \'word\' it must \'know\' what to do. For example, after you type \"3 +\", it will try to do the addition but will fail because there is only one number to be added! Here is how it must be done :
3 4 + 2 * 1 +
RIGHT!
Here is what happens. There is a pile of numbers (usually called a stack) on the floor. Each 'WORD' we write does something to the numbers on the top of that pile. We start with an empty pile. We type the word "3" and this causes the number three to be put on the top of the pile. We type the word "4" and it causes the number four to be added to the pile. The pile now contains a three on the bottom and a four on the top. Now we type the word "+" and that causes the top two numbers on the pile to be removed from the pile, added together, and the result placed back on the pile. The pile now has a single number---the number seven. We type the word "2" and it causes the number two to be added to the pile. The pile now has two numbers--seven and two. Then we type the word "*" and the top two numbers on the stack are removed, multiplied, and the result (14) is put on the pile which now contains only that one number. Then we type the words "1" and "+" which cause the number one to be put on the stack then the top two numbers (1 and 14) to be removed and added and the result (15) to be put on the pile. We are done. The answer is a single number, fifteen, and it is all by itself on the pile.
Vocabulary
- From now on we are not going to use the word "pile". We are going to call it by its proper Christian name: "Stack".
- We are not going to refer to this language as "backwards". We will call it by its proper Christian name: [Polishnotation|Postfix Polish]. It used to be called "Postfix Polish" before it became insensitive to include any nationality or race or gender in common nouns. Now it can be called ["Lukasiewicz Notation"].
- The things we type are going to be called "WORDS", even if they are numbers. A "WORD" is anything between two spaces (or any whitespace such as the start and end of lines). We typed seven words in our little example above.
Now we will see it done in the CSBuild Editor. Here is the corner of the DSA editor. For now you can ignore everything except the one line of code : 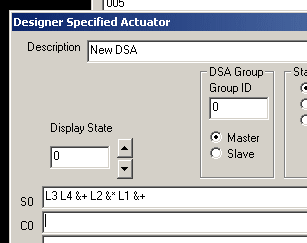 [1]
[1]
Yes, that is our sample expression that computes the number 15. You may think that it has turned ugly. You would be right. But that is what we have and the reasons are historical and boring. There are a few 'WORDS' that do not start with an ampersand, but most 'WORDS' do start with an ampersand.
In our example, we must put numbers onto the stack by using the 'L' command. "L4" means to 'Load' the number four onto the stack. "&+" means plus. Sorry about the ugliness. By clicking on the 'HELP' button, you can get a list of all the available 'WORDS' and a hint as to their meaning and how they are used. Here is a piece of that help information which includes the word "&+" : 
Notice that the name is followed by a parenthesised expression: ( x y ... x + y ). This shows the effect of the 'WORD' on the contents of the stack. The contents of the stack are shown before the operation (on the left of the ellipsis) and after the operation (right of the ellipsis). The 'x' and the 'y' are assumed to be on the stack before the &+ does its thing and the sum 'x+y' is what is on the stack afterwards. The topmost number on the stack is to the right so that in this case the 'y' is in the top and the 'x' is just below it. There may be additional numbers on the stack below the 'x' but it is not necessary for the '&+' to work properly and so is not included in the documentation for '&+'.
Now we are going to put this DSA into a program and use it to compute the number 15. We turn on tracing so that we can see the DSA in action and verify that it does, indeed, do what we want it to do. Here is the trace that is produced : =~MoveParty forward from 00(04,00)=
Object ffff stepped On pressure pad 0001 00(04,01) 000025 timer create 001 00 DLY=0000 06 00 05 01 00 00 9211d2fd Set 0x01 in DB at 00(05,01)00 000025 timer Process 001 00 DLY=0000 06 00 05 01 00 00 9211d2fd Set 0x01 in DB at 00(05,01)00 DSA Compute 15 State 0 MSG 0 (0)Execute DSA at 0(5,1) master at 0(5,1) state=0,msg=0 LOAD INTEGER 3 (3) LOAD INTEGER 4 (3 4) &+ (7) LOAD INTEGER 2 (7 2) &* (14) LOAD INTEGER 1 (14 1) &+ (15) (0)RETURN (15)~[[7]]
You can see the step-by-step execution of the program starting with the line "LOAD INTEGER 3". After each operation is performed, the trace shows the contents of the stack in parentheses. After the last operation, you can see that the stack contains the number 15, as it should. In the square brackets at the end of the trace you see that the DSA performed a total of 7 operations.
Would you believe that I have provided a sample dungeon with this DSA in it that you can play with? Well, I have and you can find it here]. I will not be doing much of this in future lessons. I will print the code and you will have to put it into your own dungeon if you want to try it out.
FAQ
- Q - "We turn on tracing (...)". But there are different tracing options to choose from the menu. Timer Trace, AttackTrace Function, Trace Monster AI, Trace Graphic Trace, and finally DSA Trace. I chose Timing Trace. It works best. What are the other Trace Options for? Did I choose the correct Trace for DSA's?
- A - The 'Timer Trace' shows the creation and processing of every timer message (Set, Clear, or Toggle). So that would be sufficient to see the timer message delivered to your DSA and any timer messages created by your DSA. But it would not show the internal operation of the DSA. In our example, we can actually see the operation of each word that is executed by the DSA and that was accomplished by turning on the "DSA Trace". The DSA Trace is treated as an addition to the Timer Trace, so in order to see the DSA Trace, you must also enable the Timer Trace.